 粒子法によるER流体中粒子の
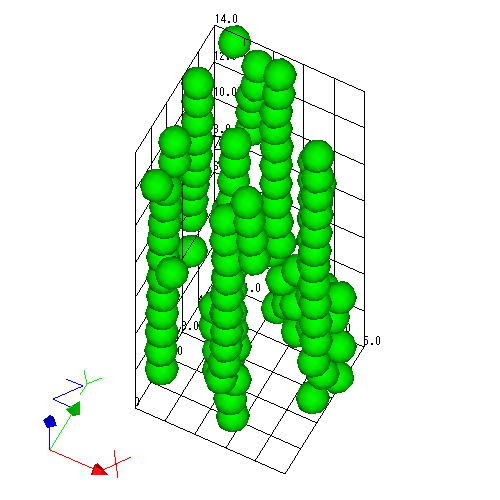
粒子法によるER流体中粒子のクラスター形成の計算結果例
 粒子法によるER流体中粒子の
粒子法によるER流体中粒子の スパイク状の界面変形現象
スパイク状の界面変形現象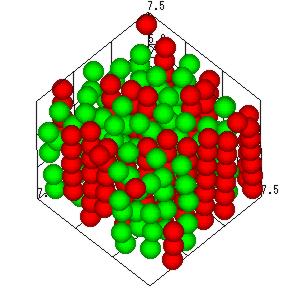 粒子法によるMAGIC砥石製作
粒子法によるMAGIC砥石製作
本研究室で行ってきた研究内容(終了したものおよび現在進行中のもの)の一部を紹介します.

機能性流体,特に磁性流体について連続体モデルとしての基礎方程式系を,熱力学的手法を用いて誘導しました.この際,磁性流体はマイクロポーラ流体としてモデル化し,電磁運動量としてAbrahamの電磁運動量を採用してE-B 対応を用いた場合と,Minkowskyの電磁運動量を採用してD-H 対応で電磁場を記述した場合を比較・検討しました.本研究で得られた方程式系において,磁化の構成方程式は従来よく用いられてきたShliomisの磁化の緩和方程式をその一部として含んでいることを示しました.
発表論文:
(1) 井門康司
「マイクロポーラ磁性流体の基礎方程式」
日本機械学会論文集, 第70巻, 第696号, B編 (2004),
pp.2065-2070.
(2) Yasushi Ido
"Basic Equations and Constitutive Equations of Magnetic Fluids With
E-B Analogy
and the Abraham Expression of
Electromagnetic Momentum"
JSME International Journal, Series B, Vol.48,
No.3 (2005), pp.488-493.
(3) Yasushi Ido
" Basic Equations and Constitutive Equations of Micropolar
Ferrofluids"
Proceedings of the First International Conference on Flow
Dynamics,
(2005), OS3-18 (DVD-ROM).
(4) 井門康司
「マイクロポーラ磁性流体の基礎方程式の誘導」
平成15年度磁性流体連合講演会講演論文集, (2003), pp.9-12.
磁性流体の磁場に対する界面変形を利用する場合,飛散や付着を防ぐためには表面を膜等で被覆して使用することが予想されます.そこで磁性流体を入れた容器の表面をシリコンゴムなどの弾性膜で被覆した連成系に対して,パルス磁場を印加した場合の膜面応答や磁性流体内部の流動状態をGSMAC有限要素法を用いて解析しました.弾性膜はMooney-Rivlin超弾性体としてモデル化しています.また,パルス磁場以外の入力磁場に対する連成系の応答特性について,実験および数値解析の両面からの解明を試みています.
発表論文:
(1) Yasushi Ido, Yoshiaki Gotoh, Takahiko Tanahashi and Gaku Hashimoto
"Numerical Analysis of Coupled Vibrations of Elastic Membrane and
Magnetic Fluid
Using the GSMAC Finite Element Method"
Proceedings of
12th International Symposium on Interdisciplinary Electromagnetic,
Mechanic and Biomedical Problems, (2005), pp.40-41.
(2) 井門康司,後藤善明,棚橋隆彦,橋本学
「GSMAC有限要素法による磁性流体−弾性膜連成系の数値解析」
日本AEM学会誌,Vol.13
No.4 (2005), pp.288-293.
(3) 後藤喜明,井門康司,棚橋隆彦,橋本学
「GSMAC有限要素法による磁性流体-弾性膜連成系の数値解析」
平成16年度磁性流体連合講演会講演論文集,(2004), pp.36-38.
本研究は福島大学の島田邦雄助教授との共同研究プロジェクトです.磁気混合流体をシリコンゴムに混合して作製した強磁性弾性膜のさまざまな印加磁場に対する応答特性について,実験およびGSMAC有限要素法を用いた数値解析の両面から解明を行っています.
発表論文:
(1) Yasushi Ido, Shin Ishida and Kunio Shimada
"Vibration Response of a Silicon
Rubber Membrane Contating a Magnetic Compound Fluid
Induced by an
Impulsive Magnetic Field"
Proceedings of 12th International Symposium on
Interdisciplinary Electromagnetic,
Mechanic and Biomedical Problems,
(2005), pp.54-55.
(2) Yasushi Ido, Shin Ishida, Shinichi Ohkubo and Kunio Shimada
"Responses of a
Silicon Rubber Membrane Containing a Magnetic Compound Fluid
to
Progressive Magnetic Field"
Proceedings of 12th International Symposium on
Interdisciplinary Electromagnetic,
Mechanic and Biomedical Problems,
(2005), pp.16-17.
(3) Yasushi Ido, Shin Ishida, Kunio Shimada
"Induced Wavy Motion of Magnetic
Rubber Membrane Due to Progressive Magnetic Field"
Proceedings of the 11th
French-Japanese International Seminar on Magnetic Fluids,
(2005),
pp.7-9.
(4) 井門康司,石田真,大久保慎一,島田邦雄
「磁気混合流体を含有するシリコンゴム膜の進行磁場に対する応答特性」
日本AEM学会誌,Vol.14 No.1 (2006), pp.27-32.
(5) 石田真,井門康司,島田邦雄,大久保慎一,福岡佑介
「磁気混合流体を含有する円形シリコンゴム膜のパルス磁場に対する応答特性」
平成16年度磁性流体連合講演会講演論文集,(2004), pp.13-15.
(6) 中川秀幸,井門康司,石田真,島田邦雄,棚橋隆彦
「印加磁場に対する強磁性シリコンゴム膜の応答特性」
平成17年度磁性流体連合講演会講演論文集,(2005), pp.23-26.

本研究は名古屋大学の梅原徳次教授との共同研究プロジェクトです.
MAGIC砥石の製作過程をStokesian dynamicsに基づく粒子法を用いて
解析しています.非磁性粒子である砥粒をMR流体に混合し,定常磁場
を印加した場合に生じるクラスター形成を利用して砥粒を整列させよう
という試みです.
発表論文:
(1) 井門康司,稲垣貴文,梅原徳次
「非磁性体粒子を混入したMR流体中粒子の配向特性(粒子法による数値解析)」
平成17年度磁性流体連合講演会講演論文集,(2005), pp.40-43.
(2) 梅原徳次,朱永生,井門康司
「MAGIC加工のシミュレーション」
平成17年度磁性流体連合講演会講演論文集,(2005), pp.44-45.
(3) Yongsheng Zhu, Noritsugu Umehara, Yasushi Ido and Atsushi Sato
"Computer
Simulation of Structures and Distributions of Particles in MAGIC
Fluid"
Proceedings of the 11th French-Japanese International Seminar on
Magnetic Fluids, (2005), pp.31-33.
本研究では機能性流体中の粒子の運動は粒子法で解析し,流体の
運動は差分法で解析するハイブリッド粒子法の開発を行っています.こ
れにより,粒子と流体の相互作用を考慮した解析を行うことができます.
現在,磁性流体やMR流体,ER流体などを対象とした数値解析を行って
います.特に,本研究室では機能性流体中微粒子が形成するクラスター
などのメゾスケール構造を明らかにするとともに,機能性流体研磨に注
目した研究を行っています.
発表論文:
(1) 深見尚男,井門康司
「ハイブリッド粒子法を用いたER流体中微粒子の電場下における応答解析」
平成17年度磁性流体連合講演会講演論文集,(2005), pp.48-51.
(2) Yasushi Ido and Hisao Fukami
"Numerical Simulation of Cluster Formation in Vibration Shear Flows
of ER Suepensions"
Asia-Pacific Symposium on Applied Electromagnetics and Mechanics,
Digest Book, (2006), p.74.

DANを構成するリン酸基が負に帯電しているため,DNA 全体としても負に帯電しています.そのため,一様定常電場を印加するとDNAは電気泳動します.この現象は分子量の異なるDNAを分離するのに利用されています.このような電気泳動現象を粒子法を用いて解析しています.
発表論文:
(1) 岩坪和英,井門康司
「DNAの電気泳動の数値解析」
日本機械学会東海支部第55期総会・講演会講演論文集, No.063-1 (2006), pp.341-342.

磁性流体やMR流体,磁気混合流体などの磁気機能性流体の液滴に磁場を印加すると界面が変形することが知られています.一例は本ホームページTOPにも取り上げているスパイク状の界面変形です(下図).本研究室では,磁気機能性流体の界面変形現象の基本的な特性を実験・数値解析によって解明するとともに,このような現象を利用した応用の開発を目指しています.